受限玻尔兹曼机的实现及其在推荐系统中的应用

受限玻尔兹曼机(restricted Boltzmann machine, RBM)是一种可通过输入数据集学习概率分布的随机生成神经网络，在降维、分类、协同过滤、特征学习和主题建模等领域中有着广泛应用。

在Netflix Prize后半程，有选手将RBM应用在该预测电影评分问题上并取得了不错的效果。后来Edwin Chen的文章《Introduction to Restricted Boltzmann Machines》使用详细而易懂的方式(没什么数学公式与推导)描述了RBM的运作机理，并使用Python的numpy写了一个简易实现。

这篇文章通过逐行阅读并运行Edwin Chen的开源代码，观看其中用到的数据结构、值的变化来展现RBM的运作原理及实现技巧。

这里仍然把背景放到音乐这里来，使用六首歌曲来训练RBM，其中三首为Disco歌曲：ABBA的Dancing Queen，Bee Gees的Stayin’ Alive，新裤子的别再问我什么是迪斯科，另外三首是吉他英雄的solo：Dire Straits的Sultans Of Swing，Yngwie Malmsteen的Black Star和桶哥Buckethead的Thorne Room。

作为一个神经网络，RBM有可见层和隐藏层两层，其中可见层每个节点对应一首歌曲，而隐藏层的每个节点我们则希望它对应于一种音乐类型，故对应上述歌曲的特点在说明中使隐藏层为两个节点。同时再加一个bias unit来控制太过热门的item对该模型造成的影响，此神经网络各节点的连接情况是这样的：

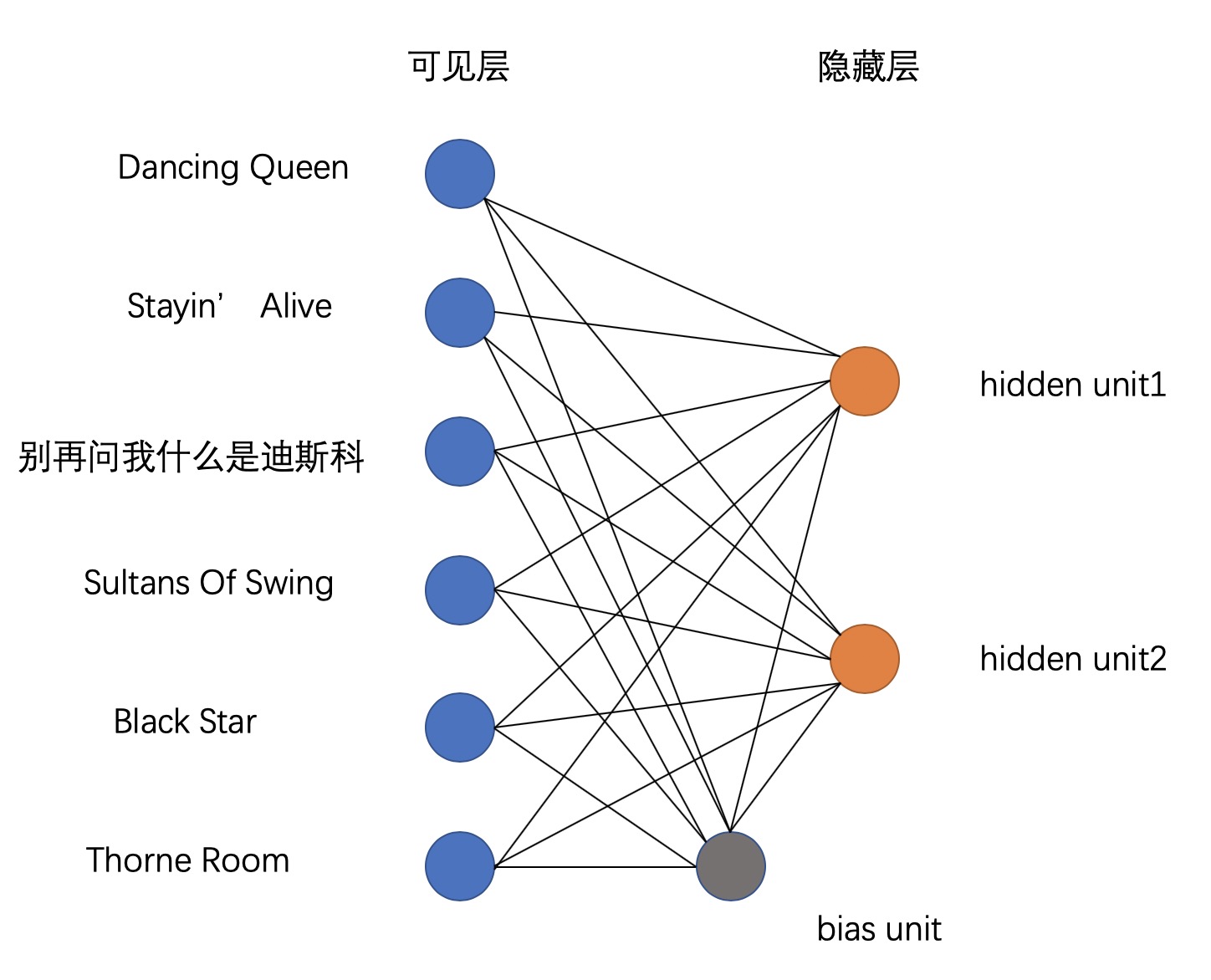
可见层的每个节点与所有隐藏层的节点相连，bias unit与两层所有的节点相连，每个连接对应一个weight，首先使用矩阵来表示可见层与隐藏层节点的所有weight，比如该矩阵的第一行的第一列的数据对应于可见层节点Dancing Queen与hidden unit1相连的weight，然后在此基础上，插入bias unit的weight，因为它与可见层、隐藏层皆相连，故此矩阵的行与列各加1。给两层节点之间的所有weight赋予一个范围内的随机值以初始化该矩阵，与bias unit相连的节点暂全置为0。

import numpy as np


num_hidden = 2
num_visible = 6
np_rng = np.random.RandomState(1234)

weights = np.asarray(np_rng.uniform(
                low=-0.1 * np.sqrt(6. / (num_hidden + num_visible)),
                high=0.1 * np.sqrt(6. / (num_hidden + num_visible)),
                size=(num_visible, num_hidden)))
weights

array([[-0.0534304 ,  0.02114986],
       [-0.01078587,  0.04942556],
       [ 0.04849323, -0.03938812],
       [-0.03871753,  0.05228579],
       [ 0.07935206,  0.06511344],
       [-0.02462677,  0.00017236]])

# 加入bias unit.
weights = np.insert(weights, 0, 0, axis=0)
weights = np.insert(weights, 0, 0, axis=1)
weights

array([[ 0.        ,  0.        ,  0.        ],
       [ 0.        , -0.0534304 ,  0.02114986],
       [ 0.        , -0.01078587,  0.04942556],
       [ 0.        ,  0.04849323, -0.03938812],
       [ 0.        , -0.03871753,  0.05228579],
       [ 0.        ,  0.07935206,  0.06511344],
       [ 0.        , -0.02462677,  0.00017236]])

接下来构造一些训练样本，一个样本是关于这六首歌的收听情况的list(按照上图从上到下的顺序对应list中的index)，填值1表示该user听过此歌，填值0表示该user未听过此歌。这里构造6个样本作为样本集合，同时考虑到weight矩阵增加了bias unit，为了后续线性代数运算的对应性，需要在样本集合形成的矩阵中再插入一列，值均置为1。

data = np.array([[1,1,1,0,0,0],[1,0,1,0,0,0],[1,1,1,0,0,0],[0,0,1,1,1,0], [0,0,1,1,0,0],[0,0,1,1,1,0]])
num_examples = data.shape[0]
data = np.insert(data, 0, 1, axis=1)

data

array([[1, 1, 1, 1, 0, 0, 0],
       [1, 1, 0, 1, 0, 0, 0],
       [1, 1, 1, 1, 0, 0, 0],
       [1, 0, 0, 1, 1, 1, 0],
       [1, 0, 0, 1, 1, 0, 0],
       [1, 0, 0, 1, 1, 1, 0]])

有了输入矩阵与weight矩阵，对于一个隐藏节点，计算它的值是1还是0，首先要将所有与它相连的节点的取值各自乘以相应的weight再做加和，比如对于靠上的隐藏节点，当输入第一个样本时，可见层的取值为[1, 1, 1, 1, 0, 0, 0]，相应的权重为[0, -0.0534304, -0.01078587, 0.04849323, -0.03871753, 0.07935206, -0.02462677]，两向量做点乘正好对应了上面的过程，注意两向量第一个值对应于bias unit，而bias unit的weight为0，对结果并未产生影响。

对于所有样本和所有的隐藏节点都是一样的处理，那么可将这么许多次点乘化为矩阵相乘，根据矩阵相乘的规则(行向量点乘列向量结果放在相应的位置)可以看出将data与weight矩阵相乘刚好表示对每个样本和每个隐藏节点将上述处理做了一次，会产生出一个新的形状为(6*3)的矩阵，第一列对应bias unit值全为0，第二列的第一个元素便对应了Dancing Queen在hidden unit1处生成的值。使用矩阵相乘，效率要比对样本和隐藏单元进行迭代快得多。

1
2
3

pos_hidden_activations = np.dot(data, weights)

pos_hidden_activations

array([[ 0.        , -0.01572304,  0.0311873 ],
       [ 0.        , -0.00493717, -0.01823826],
       [ 0.        , -0.01572304,  0.0311873 ],
       [ 0.        ,  0.08912777,  0.07801112],
       [ 0.        ,  0.00977571,  0.01289768],
       [ 0.        ,  0.08912777,  0.07801112]])

算出激活值后，众所周知，神经网络的节点往往包含一个激活函数，这里使用Sigmond函数，将上一步算出的激活值控制到0-1之间，来代表此节点被激活的可能性，当为某节点计算出的激活概率越接近1，则其被激活的可能性越大，这里利用numpy的广播功能，对上述生成的矩阵中的所有节点都施加一个Sigmond函数。然后将bias unit对应的那一列全改为1，这表示bias unit总是被激活的，具体原因见下文。

def logistic(x):
    return 1.0 / (1 + np.exp(-x))

pos_hidden_probs = logistic(pos_hidden_activations)
pos_hidden_probs[:, 0] = 1
pos_hidden_probs

array([[1.        , 0.49606932, 0.50779619],
       [1.        , 0.49876571, 0.49544056],
       [1.        , 0.49606932, 0.50779619],
       [1.        , 0.5222672 , 0.5194929 ],
       [1.        , 0.50244391, 0.50322437],
       [1.        , 0.5222672 , 0.5194929 ]])

rand函数会随机生成一个处于0到1之间的数，将上述算出的节点激活概率与一个这样的随机数比较大小来决定是否激活此节点，这意味着即使此时某次训练中某隐藏结点的激活概率为0.99，也是有可能不被激活的。

1 2	pos_hidden_states = pos_hidden_probs > np.random.rand(num_examples, num_hidden + 1) pos_hidden_states

array([[ True,  True,  True],
       [ True, False, False],
       [ True, False, False],
       [ True,  True,  True],
       [ True, False,  True],
       [ True, False,  True]])

这个矩阵的含义举例为其第一行第二列的值表示Dancing Queen是否激活了hidden unit1。

如上述进行过了一次所有样本对隐藏层激活情况的计算，可以得出Dancing Queen与hidden unit1同时亮起的相关性，记为$Positive(e_{ij})$，看上述矩阵data与pos_hidden_probs，第一个样本在Dancing Queen节点取值为1，对hidden unit1激活概率为0.49606932，将两者相乘得到一个值，对所有样本如此计算得到的值的加和即为这两个节点的相关性，这个过程同样可以使用矩阵相乘来表示如下：

1 2	pos_associations = np.dot(data.T, pos_hidden_probs) pos_associations

array([[6.        , 3.03788267, 3.05324311],
       [3.        , 1.49090435, 1.51103295],
       [2.        , 0.99213864, 1.01559239],
       [6.        , 3.03788267, 3.05324311],
       [3.        , 1.54697831, 1.54221017],
       [2.        , 1.04453441, 1.03898579],
       [0.        , 0.        , 0.        ]])

如此，一次从可见层到隐藏层的计算便结束了。之后反过来，从隐藏层到可见层，将pos_hidden_states作为样本集合输入隐藏层，做一遍与上述过程完全相同的计算，同样可以计算出两相连节点之间的相关性，这次记为$Negative(e_{ij})$。由于是随机取的初始weight，Positive与Negative之间应该会有不小的差别，而RBM的优化目标便是通过多个epoch的训练，使其差别尽可能小。

上述一正一反便算完成了一个epoch，根据式子$w _ { i j } = w _ { i j } + L * \left( \text {Positive} \left( e _ { i j } \right) - N e g a t i v e \left( e _ { i j } \right) \right)$算出新的weight值(其中L为学习速率需要炼金而得)，来开始下一个epoch的计算，如此会使得两者之间的差值越来越小，从而得到一个训练好的RBM模型。

比较巧妙的还是bias unit，可以看到上述有些可见节点与bias unit的关联值达到6，而在下一次循环中，又会对bias unit整个重新赋值，这个处理可以将那些热门的item对隐藏节点是否激活的影响引向这个bias unit，来稀释这种影响，尽量防止“the Beatles现象”的出现。同时，由于它与两层每个节点都相连，在从可见层到隐藏层的计算过程中，它其实是作为一个隐藏层节点来一同参与计算的，而在反向时，它又作为一个可见层节点来发挥作用，真是妙啊。

使用上述过程的完整版代码(见文末参考链接)，来看一下结果：

r = RBM(num_visible = 6, num_hidden = 2)
training_data = np.array([[1,1,1,0,0,0],[1,0,1,0,0,0],[1,1,1,0,0,0],[0,0,1,1,1,0], [0,0,1,1,0,0],[0,0,1,1,1,0]])
r.train(training_data, max_epochs = 5000)
print(r.weights[1:, 1:])

[[-8.09650002  3.95552071]
 [-5.45512759  1.42845858]
 [ 1.74474585  4.06127352]
 [ 7.74906751 -3.54062571]
 [ 3.18686136 -7.33215302]
 [-2.46868951 -2.60826581]]

从训练好的weight中可以看出，hidden unit1倾向于对应rock guitar hero的音乐，而hidden unit2则倾向于对应disco。

联系推荐系统，显然该模型可以对item做降维处理，与Word2vec一样，使用weight组成的向量表示即可，比如Dancing Queen可表示为[-8.09650002, 3.95552071]。
而要为user推荐item，则需要将其收听历史向量[1, 1, 1, 0, 0, 0]输入训练好的模型，激活一些隐藏节点，再将表示隐藏层节点被激活情况的向量反向输入模型，可为每个item得到一个被激活的概率，去掉用户已经听过的item，再对概率进行从大到小排序选取K个即可做出TopK推荐。该处理只有简单的向量计算非常迅速，可用于在线实时生成推荐结果。

对于显示反馈，比如Netflix Prize的情况，Ruslan Salakhutdinov等人对RBM提出了改进，可见层使用Softmax神经元来表示打分情况，对于没有被评分过的item则使用特殊的神经元表示，不与隐藏层相连避免无谓的计算；而条件RBM可以在处理显示反馈时将用户浏览过哪些物品这样的隐式反馈的影响同时考虑进去。这些改进都涉及到对本文计算过程与数学公式的改进，具体可以参考论文。

参考

echen/restricted-boltzmann-machines
Introduction to Restricted Boltzmann Machines
Restricted Boltzmann Machines for Collaborative Filtering

Contents

参考